This year I decided to teach factoring trinomials algebraically first, then with Algebra tiles. Today was their first day (ever) with the tiles. There is certainly a learning curve for students when working with Algebra tiles. My students claim they never saw such a thing....it's possible.
Today we only worked with x^2 + bx + c where b and c were positive numbers.
I gave some rules:
1) Begin building your rectangle with the x^2 square in the upper left of your work area.
2) Build off your x^2 with x rectangles to the right and down.
3) Fill in the bottom right of your rectangle with the 1 squares.
4) You must create a rectangle (no holes).
Before class started I downloaded this template for algebra tiles, copied them on different color paper, cut them out myself (because my students take forever to cut), and bagged them in Ziplock bags. In hindsight, I should have used red and green paper to use later with negative and positive.
Next, I needed to make sure that the students have enough tiles to create the rectangles.
Here are all the trinomials that will work this this tile template:
x^2 + 2x + 1 = (x + 1)(x + 1)
x^2 + 3x + 2 = (x + 1)(x + 2)
x^2 + 4x + 4 = (x + 2)(x + 2)
x^2 + 5x + 6 = (x + 2)(x + 3)
x^2 + 6x + 9 = (x + 3)(x + 3)
x^2 + 7x + 12 = (x + 3)(x + 4)
x^2 + 8x + 16 = (x + 4)(x + 4)
x^2 + 4x + 3 = (x + 1)(x + 3)
x^2 + 5x + 4 = (x + 1)(x + 4)
x^2 + 6x + 5 = (x + 1)(x + 5)
x^2 + 7x + 6 = (x + 1)(x + 6)
x^2 + 8x + 7 = (x + 1)(x + 7)
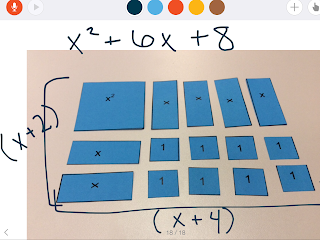
x^2 + 6x + 8 = (x + 2)(x + 4)
x^2 + 7x + 10 = (x + 2)(x + 5)
x^2 + 8x + 12 = (x + 2)(x + 6)
x^2 + 8x + 15 = (x + 3)(x + 5)
It takes the students a few tries and a few reminders of the rules, but eventually they get it.
Here are a few examples we did:
Today we only worked with x^2 + bx + c where b and c were positive numbers.
I gave some rules:
1) Begin building your rectangle with the x^2 square in the upper left of your work area.
2) Build off your x^2 with x rectangles to the right and down.
3) Fill in the bottom right of your rectangle with the 1 squares.
4) You must create a rectangle (no holes).
Before class started I downloaded this template for algebra tiles, copied them on different color paper, cut them out myself (because my students take forever to cut), and bagged them in Ziplock bags. In hindsight, I should have used red and green paper to use later with negative and positive.
Next, I needed to make sure that the students have enough tiles to create the rectangles.
Here are all the trinomials that will work this this tile template:
x^2 + 2x + 1 = (x + 1)(x + 1)
x^2 + 3x + 2 = (x + 1)(x + 2)
x^2 + 4x + 4 = (x + 2)(x + 2)
x^2 + 5x + 6 = (x + 2)(x + 3)
x^2 + 6x + 9 = (x + 3)(x + 3)
x^2 + 7x + 12 = (x + 3)(x + 4)
x^2 + 8x + 16 = (x + 4)(x + 4)
x^2 + 4x + 3 = (x + 1)(x + 3)
x^2 + 5x + 4 = (x + 1)(x + 4)
x^2 + 6x + 5 = (x + 1)(x + 5)
x^2 + 7x + 6 = (x + 1)(x + 6)
x^2 + 8x + 7 = (x + 1)(x + 7)
x^2 + 6x + 8 = (x + 2)(x + 4)
x^2 + 7x + 10 = (x + 2)(x + 5)
x^2 + 8x + 12 = (x + 2)(x + 6)
x^2 + 8x + 15 = (x + 3)(x + 5)
It takes the students a few tries and a few reminders of the rules, but eventually they get it.
Here are a few examples we did:
After about 5 or 6 examples of this, I gave them a challenge. 2x^2 + 7x + 6



I created this activity on Desmos for playing with Algebra Tiles and factoring, check it out.
ReplyDeletehttps://teacher.desmos.com/activitybuilder/custom/56c059e999f874042c304cca
That's pretty cool! Great way to not have all those little pieces of paper all over the floor.
Delete